Startsidan | Kursöversikt | Epost till läraren | Hjälp

Ersättningsresistanser

Elektriska kretsar kan innehålla många olika komponenter. Man kan göra en krets enklare att beräkna och förstå om man kan ersätta flera komponenter med en som har samma verkan.

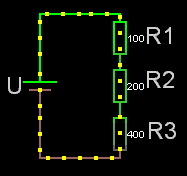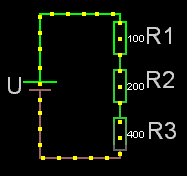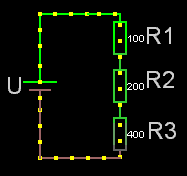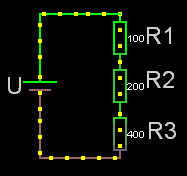
Seriekopplade

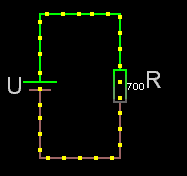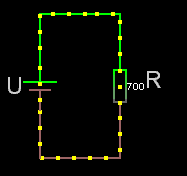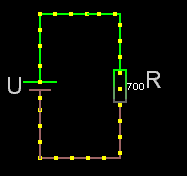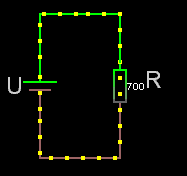
3 serie resistorer. 1 ersättning för 3 R

För seriekopplade resistorer gäller det enkla förhållandet att man adderar resistanserna. Rserie = R1+R2+osv.

Obs! För seriekopplade resistorer är sammanlagda resistansen alltid större än den största av dem ingående.

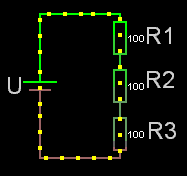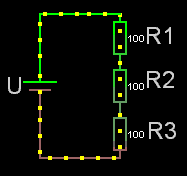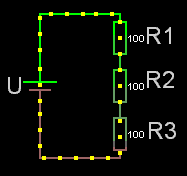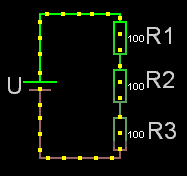
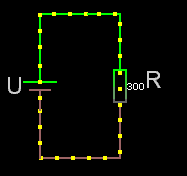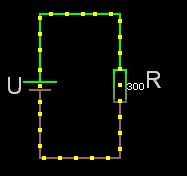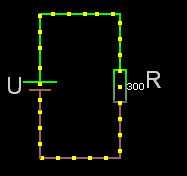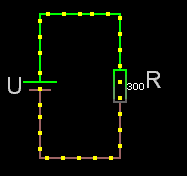
3 lika serie resistorer 1 ersättning för de 3 R
Om det är lika stora seriekopplade resistorer är:

sammanlagda resistansen = Ren * antalet

Parallellkopplade

3 olika parallella resistorer 1 ersättning för 3 parallella R
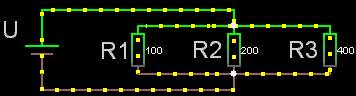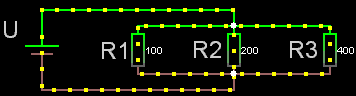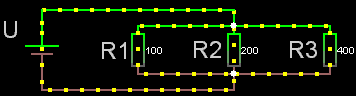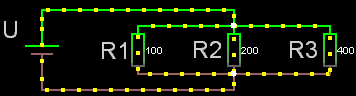
För parallellkopplade resistorer gäller:
1/Rparallell = 1/R1 + 1/R2 + 1/R3 o.s.v.

Ett vanligt fel är att glömma att invertera 1/R efter uträkningen för att få R. Man kan utnyttja:

Rparallell=1/ (1/Rparallell)

och direkt ställa upp: Rparallell = 1/(1/R1 + 1/R2 + 1/R3 o.s.v.)

Om man har just 2 resistorer kan man skriva:
1/R = 1/R1 + 1/R2 = (1·R2)/(R1·R2) + (R1·1) /(R1·R2) = (R1+R2)/(R1R2)

så om vi inverterar:

R1&2parallell = (R1R2)/(R1+R2)

Obs! För parallellkopplade resistorer är sammanlagda resistansen alltid mindre än den minsta av de ingående.

3 lika parallella resistorer 1 ersättning för 3 parallella R
Om det är lika stora parallellkopplade resistorer är:
sammanlagda resistansen = Ren/antalet

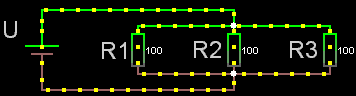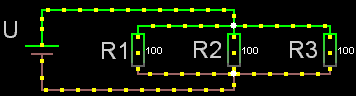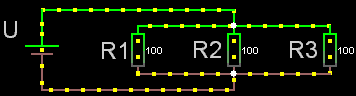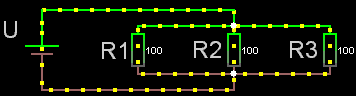
Både parallell- och serie-koppling


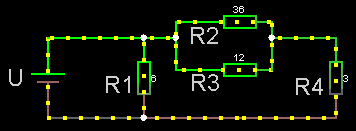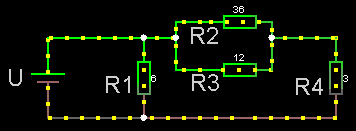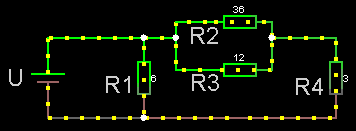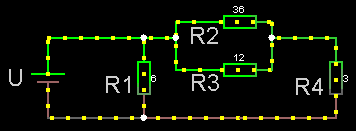
Man kan alltid försöka hitta ett par (eventuellt flera) resistorer som antingen är:
  * i serie (= hela strömmen går genom samtliga resistorer eftersom de är kopplade efter varandra).
  * parallellkopplade (= strömmen delar upp sig i delströmmar som var och en går genom sin resistor eftersom de olika resistorerna utgår från samma punkt och "möts" i en gemensam punkt). Sådana par kan man räkna på var för sig för att ersätta dem med en ersättningsresistans, som i sin tur kan bli en del i ett nytt par.

För kretsar där det inte går att dela upp så måste man tillämpa Kirchoffslagar.

Kondensatorer

som resistorer fast tvärtom:
För seriekopplade kondensatorer (kallas även "kapacitanser") gäller:
1/Cserie = 1/C1 + 1/C2 + 1/C3 o.s.v.
För parallellkopplade kondensatorer gäller:
Cparallell = C1+C2+osv.

De animerade bilderna på denna sida har gjorts med Falstads java kretssimulator.

2005 Nationellt centrum för flexibelt lärande