I många kretsar kan man enkelt sätta ihop resistorer och andra komponenter till enklare ersättningar och få en krets som är lättare att räkna på.
Men ibland är kretsen så sammanflätad att man behöver Kirchoffs lagar för att få rätsida på problemet.
Första steget är att markera strömmarna med en riktning, I 1 I 2 och så vidare. Det spelar ingen roll om en eller flera strömmar skulle tilldelas fel riktning. I den framräknade lösningen kommer dessa då få ett negativt värde.
Nu kan Du markera spänningsfall, I·R, över resistorerna. Det blir en högre spänning där strömmen går in i resistorn.
Kirchoffs spänningslag (summan av alla spänningar när man går runt en krets är 0. Man kan gärna dela upp kretsen i olika "maskor" som i en stickning.).
1 - 2·I1 - 3·I2
= 0
5 + 4·I3 - 3·I2
= 0
Kirchoffs strömlag: Summan av alla strömmar in mot en förbindningspunkt
är lika med summan av strömmarna ut från förbindningspunkten.
(Man kan också uttrycka det som: summan av alla strömmar i en
förbindningspunkt är 0, strömmar på väg in mot
punkten tas med "+"-tecken, strömmar på väg ut från
punkten tas med "-"-tecken)
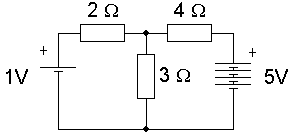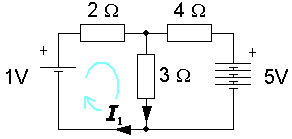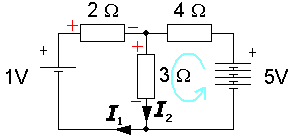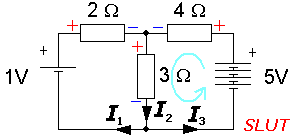
I2 = I1+ I3
Snygga till (lägg I1, I2, I
3 och konstanter i ordning), och Du får dessa tre ekvationer:
(1) I1 - I2
+ I3 = 0
(2) 2I1 + 3I2 +
0 = 1
(3) 0 + 3I2
+ 4I3 = 5
Detta linjära ekvationssystem löses. Om du är osäker hur du skall göra det så kolla lösa ekvationssystem. Strömmarna blir:
I1 = -4 / 13 ≈ -0,307 A; I2 = 7 / 13 ≈ 0,5384 A; I 3 = 11 / 13 ≈ 0,8461 A
Genom att peka på en komponent (ledare, resistor, batteri) med musen tills den blir blå, kan man avläsa, bland annat, strömmen, I, genom komponenten i nederdelen av appleten.
Den vänstra kretsen är precis som den som räknades ovan.
I den högra kretsen har en egenskap hos en komponent ändrats som gör att ström byter riktning i en del av kretsen. Vad har ändrats? Svar:
Hur stor är spänningsfallet över den komponenten i de
två fallen?
Tips
1 (Alla)
Svar:
Om du högerklickar i appletten kan du välja circuits > CFL > och därunder potential eller mardröm. Överhuvudtaget kan du påverka denna simulering på en massa sätt. Se Kretssimulator 2!
 Atomen
Atomen
 Kretsteori
Kretsteori