Skriv utHastighet
Här skall vi studera en rörelse och hur läge – tid respektive hastighet – tid grafen ser ut för samma rörelse.
Vi skall också se hur man kan bestämma momentanhastigheten i en viss tidpunkt för samma rörelse på några olika sätt.
Hastighet definieras som
|
Kör filmen för att bekanta dig med den.
Vi har mätt upp bilens läge vid varje tidpunkt.
Tabell
med mätvärden.
Vi kan nu göra en läge–tid-graf av dessa mätvärden. (y- axeln är i (m) och x- axeln i bildrutor med 0,04 s mellan.)
Momentanhastighet
Vi skall nu se hur man kan bestämma bilens momentanhastighet i en
viss tidpunkt.
Vi har valt t = 1,00 s.
Vi söker momentanhastigheten vid tidpunkten t = 1,00 s. (s = 1,309 m)
Ett sätt är att mäta läget lite före, här 5 rutor före, t = 0,80 s. (s1 = 0,978 m)
och 5 rutor efter aktuellt läge, t = 1,20 s. (s2 = 1,541 m)
Och sedan använda formeln
- v = hastighet
- s = läge
- t = tid
Vi hoppas då att den medelhastighet vi får fram är ett bra mått på momentanhastigheten i önskad punkt.
För att få ett ännu bättre värde på medelhastigheten så väljer vi bilder som ligger ännu närmare tidpunkten.
Men då får vi ett problem, för ju närmare punkten vi kommer desto mindre blir skillnaden i läge, och desto mer inverkar avläsningsfelen.
En ruta före t = 0,96 s. (s1 = 1,249 m)
En ruta efter, t = 1,04 s. (s2 = 1,367 m)
1 centimeters felavläsning på sträckan 25 cm gör ett fel på 4 % medan 1 cm fel då sträckan är 5 cm gör ett fel på hela 20 %.
Vi får alltså göra en avvägning mellan:
- Ett stort intervall. Beräknad hastighet blir inte så nära momentanhastigheten i punkten.
- Ett litet intervall. Svårigheten att avläsa noggrant kommer att spela en allt större roll.
Grafiskt kan vi visa vad vi gör:
0,2 s före och 0,2 s efter vald tidpunkt.
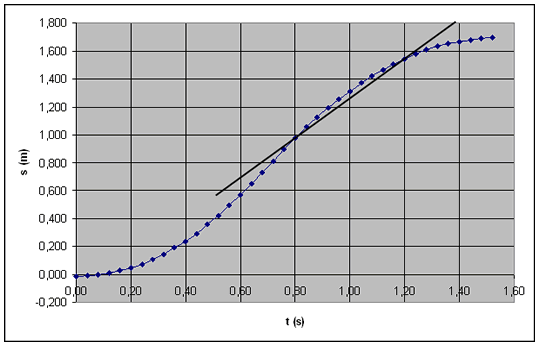
0,04 s före och 0,04 s efter vald tidpunkt
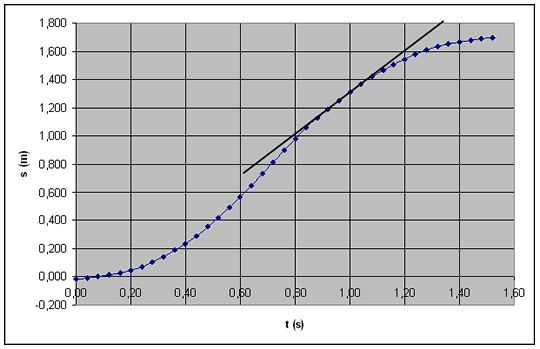
Om vi i tanken låter våra punkter närma sig den valda tidpunkten (1,0 s) så kommer sekanten (linjen som skär en kurva i två punkter) ovan att övergå i en tangent (linje som rör kurvan i bara en punkt).
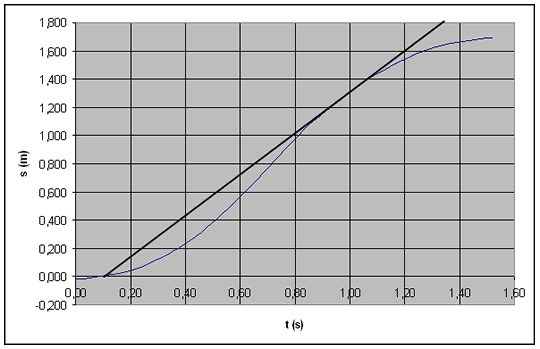
Övning: Beräkna tangentens lutning.
Svar:
Svar: 1,45 m/s t.ex. v = delta s/delta t = (1,60-0,00)/(1,20-0,10)