Area | Volym

Areaberäkning

Nedanstående formler samt en massa andra finns även i din formelsamling. Formlerna för triangelns, rektangelns och cirkelns area bör du kunna utantill när kursen är slut. De andra formlerna skall du kunna använda dig av vid behov.

Trianglar | Rektangel | Cirkel | Sammansatta figurer

Trianglar

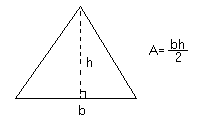Exempel: Om b= 8 cm och h=7 cm, hur stor är arean då? A = bh/2 = 8*7/2 cm2 Svar: Arean är 28cm2

Rektangel

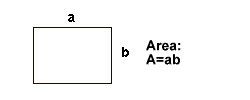Exempel: Om a= 7 km och b= 5 km, hur stor är arean då? A = ab = 7*5 km2 Svar: Arean är 35 km2

Cirkel

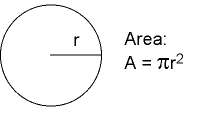Exempel: Om r= 10,0 mm, hur stor är arean då? A = pr2 = 100p mm2 Svar: Arean är ca 314 mm2

Sammansatta figurer

Det finns inga färdiga formler utan det gäller det att kombinera ihop en egen formel för arean. Hur den skall vara beror naturligtvis på vilka "grundfigurer" ytan består av.
 

Volymsberäkning

Rätblock | Cylinder | Sfär | Sammansatta kroppar

Nedanstående formler samt en massa andra finns även i din formelsamling. Formlerna för rätblockets, cylinderns och sfärens volym bör du kunna utantill när kursen är slut. De andra formlerna skall du kunna använda dig av vid behov.

Rätblock

Ett rätblock är som "en vanlig låda", sex plana sidor och räta vinklar mellan sidorna.

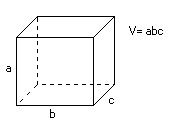Exempel: Hur stor volym har en flytt-kartong med måtten: b= 6,0 dm (längd), c= 4,5 dm (djup) och a= 5,0 dm (höjd)? V= abc= 5,0*6,0*4,5 dm3 Svar: Flyttkartongens volym är ca 140 dm3

Cylinder

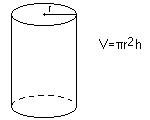Exempel: En tank som invändigt har formen av en rak cirkulär cylinder har radien 0,7 m och längden 3,2 m. Hur stor volym ryms i tanken? V=pr2h=p0,72*3,2 m3 Svar: Tanken rymmer ca 4,9 m3

Sfär

En sfär är som en perfekt rund kula eller boll.

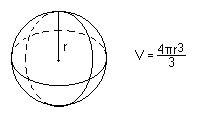Exempel: Hur stor volym har en kula med radien 0,50 cm? V=4pr3/3 = 4*0,503p/3 cm3 Svar: Volymen är ca 0,52 cm3

Sammansatta kroppar

Här finns inga färdiga formler utan här gäller det att kombinera ihop en egen formel för volymen. Hur formeln skall vara beror naturligtvis på vilka "grundfigurer" kroppen består av.