För en rätvinklig triangel med katetlängderna (de korta sidornas längder) a och b och hypotenusans längd (den längsta sidan) c gäller sambandet a² + b² = c².

Detta samband är känt som Pythagoras sats. Det gäller även "baklänges" dvs man kan kolla om en given triangel är rätvinklig genom att använda värdena på a, b och c och se om HL = VL. Det här sambandet var känt redan av de gamla babylonierna för ca 4 000 år sedan, 1 500 år före Pythagoras levde.

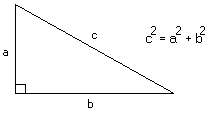Exempel: En triangel har sidlängderna 6 cm, 8 cm och 10 cm. Är triangeln rätvinklig? a2+b2 =62+82 =36+64 =100 c2 =102 =100 I detta fall är a2+b2 =c2 (för 100 =100) Svar: Triangeln är rätvinklig.