|
Trigonometrin var från början ett sätt att
beräkna avstånd genom att mäta vinklar och
utnyttja kunskap om likformiga trianglar. Det finns fler användningsområden
för trigonometriska funktioner men det tas inte upp i
denna kurs.
Cosinus
| Sinus
| Tangens
Cosinus
|
Cosinus
för vinkeln v skrivs cos v
cos
v
är ett tal mellan -1 och 1. I Matematik A finns
bara tillämpningar där cos v är
mellan 0 och 1.
|
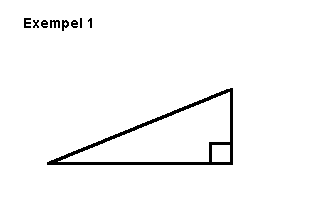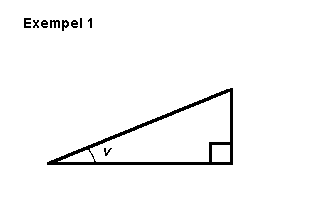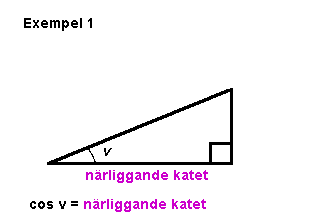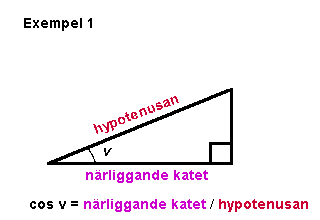
|
|
|
Funktionen
cos v är alltså användbar i problem där
vinkeln v, närliggande
katet (kortsidan vid vinkeln v) och hypotenusan
(triangelns längsta sida) är kända. |
Vill
man beräkna hur stor en
vinkel v är och man
vet hur lång den närliggande
kateten och hypotenusan
används inversfunktionen arccos v.
På
miniräknaren betecknas detta cos-1,
den funktionen är på samma tangent som cos v.

Sinus
|
Sinus
för vinkeln v skrivs sin v
sin
v
är ett tal mellan -1 och 1. I Matematik A finns
bara tillämpningar där sin v är
mellan 0 och 1.
|
|
|
|
Funktionen
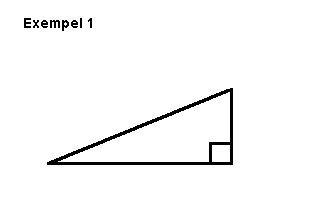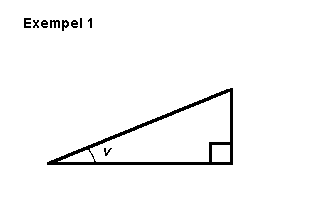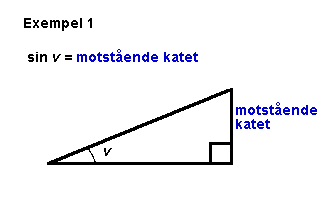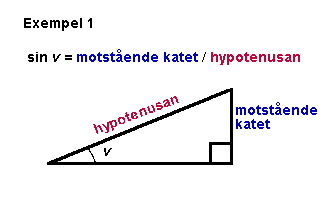
sin v är alltså användbar i problem där
vinkeln v, motstående
katet (kortsidan längst bort från vinkeln
v sett) och hypotenusan (triangelns
längsta sida) är kända. |
Vill
man beräkna hur stor en
vinkel v är och man
vet hur lång den motstående
kateten och hypotenusan
används inversfunktionen arcsin
v.
På
miniräknaren betecknas detta sin-1,
den funktionen finns på samma tangent som sin v.

Tangens
|
Tangens
för vinkeln v skrivs tan v
tan
v
är ett tal mellan oändlgheten och "minus
oändligheten". I Matematik A finns bara tillämpningar
där tan v är mellan 0 och oändligheten.
|
|
|
|
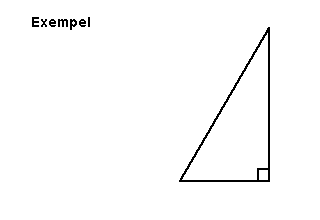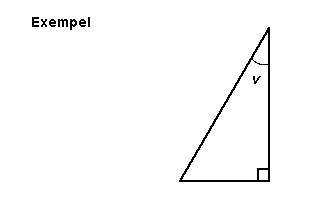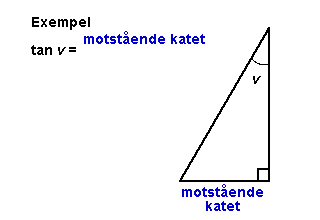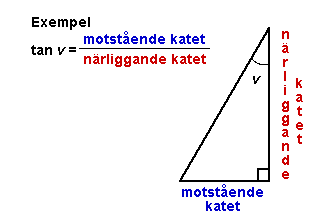
Funktionen
tan v är alltså användbar i problem där
vinkeln v, motstående
katet (kortsidan längst bort från vinkeln
v sett) och närliggande katet
(kortsidan närmast vinkeln v) är
kända. |
Vill
man beräkna hur stor en
vinkel v är och man
vet hur lång den motstående
kateten och närliggande
katet används inversfunktionen
arctan v.
På
miniräknaren betecknas detta tan-1,
den funktionen finns på samma tangent som tan v.
Här
kan du få ett övningsblad att trycka som tränar dig på att
hitta rätt samband (sinus, cosinus eller tangens)
och sätta in det i en ekvation på rätt sätt för att hitta
en viss sida eller vinkel: TrigGrund.pdf

|