|
Spetsig
vinkel | Rät vinkel
| Trubbig vinkel
Vinkelsummor i flerhörningar
| Yttervinkelsatsen
Spetsig
vinkel
Om
vinkeln är mindre än 90 grader är det en spetsig
vinkel.


Rät
vinkel
Om
vinkeln är precis 90 grader är det en rät vinkel.
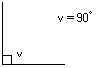

Trubbig
vinkel
Om
vinkeln är större än 90 grader är det
en trubbig vinkel.
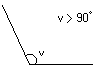

Vinkelsummor
i flerhörningar
Summan
av vinklarna kallas vinkelsumma.
- En
triangel (trekant) har alltid vinkelsumman 180 grader.
- En
fyrkant har alltid vinkelsumman 360 grader.
- En
femkant har alltid vinkelsumman 540 grader.
- En
sexkant har alltid vinkelsumman 720 grader.
Ser du
mönstret? I så fall kan du räkna ut hur stor
vinkelsumman är i en sjukant .

Yttervinkelsatsen
Det
kan ibland vara bra att använda små "genvägar"
när man löser uppgifter inom matematiken. Då
kan man slippa göra en del eget tankearbete (det gäller
då stället att hålla reda på de genvägar
som finns). De genvägar som finns brukar kallas regler
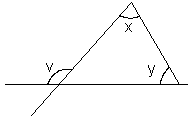
eller satser. Yttervinkelsatsen kan användas dels om
man känner yttervinkeln v samt en av de inre vinklarna
x eller y och vill räkna ut den andra inre vinkeln (y
eller x).
 |
|
Yttervinkelsatsen
v
= x + y
|
|
Försök
att själv komma fram till att denna formel stämmer
genom att utgå från följande antaganden:
- Vinkelsumman
i en triangel är 180 grader.
- Ett
halvt varv är 180 grader.

|