|
Procentuell
förändring | Förändringsfaktor
Procentuella
förändringar
Om
t ex ett pris ändras kan man prata om en absolut ökning,
dvs höjning i reda pengar, eller en relativ ökning,
dvs höjningen jämförs med vad priset var innan
ändringen. När man beräknar den procentuella
förändringen är det fråga om en relativ
ökning och svaret skall anges i procent. Du räknar
som i princip lika som vid ett procentsatsproblem.
|
Ex1
|
Priset
på en cykel höjs med 300 kr. Innan kostade
den 1500 kr. Hur stor
är den den procentuella förändringen?
Uträkning:
Prisändringen delas med det
gamla priset
300/1500
=
0,20 = 20%
Svar:
Priset har höjts med 20%
|
|
Ex
2
|
Priset
på en tröja sänks med 40 kr. Innan kostade
den 250 kr. Hur
stor
är den den procentuella förändringen?
Uträkning:
Prisändringen delas med det
gamla priset
40/250 =
0,16 = 16%
Svar: Priset har sänkts med 16%
|

Förändringsfaktorn
Att
använda förändringsfaktorn kan bespara dig
flera beräknigar och därmed mycket tid och knapptryckningar.
På så vis minskar även risken för felskrivning
eller avrundningsfel. Förändringsfaktorn används
vid procentuella förändringar, i synnerhet om det
är fråga om upprepade förändringar.
Hur
bestämmer man förändringsfaktorn om man vet
den procentuella förändringen? Gör först
om den procentuella förändringen till ett decimaltal,
sedan tar du 1 plus detta tal om det är frågan
om en höjning, är det en sänkning tar du 1
minus det tal du tog fram.
|
Ex
1
|
Priset
på en lampa höjs med 20%. Vad blir förändrings-faktorn
på priset?
Uträkning:
20% = 0,20
Höjning: 1+0,20 = 1,20
Svar: Förändringsfaktorn är 1,20
|
|
Ex
2
|
Priset
på en spis sänks med 15%. Vad blir förändrings-faktorn
på priset?
Uträkning:
15% = 0,15
Sänkning:
1-0,15 = 0,85
Svar:
Förändringsfaktorn är 0,85
|

Hur
använder man sig av förändringsfaktorn i sina
beräkningar för att spara arbete?
|
Ex
3
|
Priset
på en lampa höjs med 20%. Vad blir det nya
priset om lampan kostar 250 kr före höjningen?
Uträkning:
20% = 0,20
Förändringsfaktor:
1+0,20 = 1,20
Nytt
pris (i kr): 1,20*250 = 300
Svar:
Det nya priset är 300 kr
|
|
Ex
4
|
Du
satsar 5 000 kr på aktier och räknar med
en årlig avkastning på 14%. Vad är
aktierna värda efter 3 år?
Uträkning:
14% = 0,14
Förändringsfaktor för varje år:
1+0,14 = 1,14
Total
förändringsfaktor: 1,143
Beräknat
värde: 5000*1,143 = 7407,72
Svar:
Värdet efter tre år beräknas till ca
7407 kr
|
Ännu
fiffigare blir det när man har lärt sig använda
potenser (finns i "Grafer och funktioner",
kapitel 6 i läroboken) när det är
fråga om en ökning eller minskning som sker i samma
procentuella takt under en längre tid.

Hur
bestämmer man förändringsfaktorn om man vet
det nya och det gamla priset? Jo, man tar det nya priset och
delar med det gamla priset.
|
Ex
5
|
En
soffa kostade före prishöjning 5 900 kr. Efter
pris-höjningen kostar den 6 200 kr
Uträkning:
gammalt pris är 5 900 kr, nytt pris är 6 200
kr
Förändringsfaktorn
är 6200/ 5900 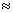 1,051
1,051
Svar:
Förändringsfakorn är 1,051
(Det nya priset är 105,1% av det gamla priset,
det nya priset är 5,1% högre än det gamla
priset)
|
|
Ex
6
|
Ett
bord kostade före prissänkning 2 800 kr. Efter
pris-höjningen kostar den 2 100 kr
Uträkning:
gammalt pris är 2 800 kr, nytt pris är 2 100
kr
Förändringsfaktorn
är 2100/ 2800=0,75
Svar:
Förändringsfakorn är 0,75
(Det nya priset är 75% av det gamla priset,
det nya priset är 25% lägre än det gamla
priset)
|
Träna på att använda förändringsfaktorn
1

|